A central goal of computational neuroscience is to account for cognitive phenomenon as emerging from the neural substrate constituting central nervous systems. An important such cognitive phenomenon is working memory, the ability to hold information about items for further processing. Attractor neural networks have been proposed to model the emergence of working memory from the interaction of neurons. In this scenario, items are encoded by patterns of activity in the network, such that an item is held in memory when the network exhibits a specific pattern of activity. With an attracting dynamics towards these specific patterns, attractor neural networks account for phenomenological aspects of working memory, such as associativity, as well as for observed neural correlates of working memory, such as persistent activity. These properties can be understood at a microscopic level: neurons that are active in a given pattern of activity are connected with each others through a synaptic connectivity that implements a feed-back loop in which neural activity can be amplified and reverberated. Theoretical models can be used to assess the efficiency with which variations on this feed-back loop mechanism implement working memory. This is typically done by computing the maximal number of items that can be held in working memory in a network.
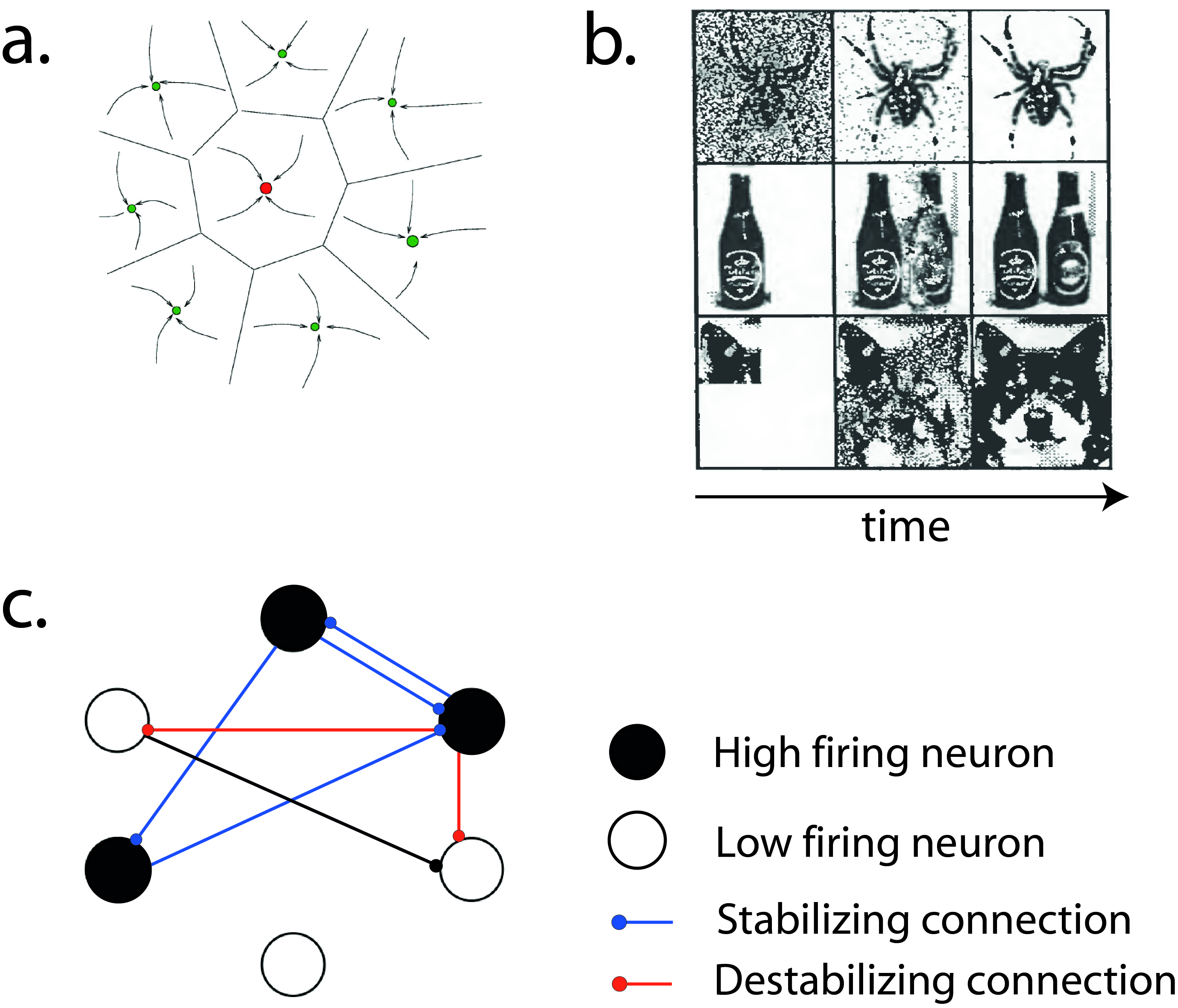
a. Schematic description of the attracting neural trajectories that are characteristics of attractor neural networks. This representation can be seen as a 2-D projection of the neural network state-space. Arrows represent neural trajectories converging towards fixed-points, the dot representing patterns of activity coding for different items.
b. These attracting trajectories account for the associative aspect of working memory: partial observation of an item triggers the recall of this item (illustrations taken from Introduction to the theory of neural computation by Hertz, Krogg and Palmer).
c. A network pattern of activity encoding an item to be memorized. Blue connections create a feed-back loop in which activity can reverberate to endow the network with a dynamical properties that can be mapped onto the phenomenology of working memory.
.
Memory and cortical connectivity
Early study of attractor neural networks have shown that minimal models were able to efficiently implement working memory. Since these early works in the 80’s new experimental data about the anatomy and physiology of neural networks have been gathered in various brain structures and a line of research consists in testing the compatibility of these new data with the attractor scenario of working memory. I have followed this line of research with Nicolas Brunel during my PhD, focusing on new experimental measurements of neural network connectivity. One observation is that biological synapses can take only a small discrete number of values, as opposed to the graded values taken by synapses in early neural network models. Taking this fact into account we have shown that the attractor scenario is well suited to account for the ability of local circuits of the hippocampus and cerebral cortex to implement working memory.
Abstract items are known to be encoded in a distributed manner across the cortical surface. Whether a distributed set of cortical areas can function as an attractor neural network is unknown. To address this question, we studied a large-scale modular model of cortical networks and showed that experimental characterizations of large-scale cortical structures are consistent with the idea that distributed cortical areas implement attractor dynamics.
Anatomical and physiological studies show that cortical areas are organized in a hierarchical manner with respect to the sensory inputs received from the thalamus. I have extended the large-scale model described above to introduce a notion of hierarchy, which allowed me to characterize how the organization of a hierarchical structure impact the memory performance of a network.
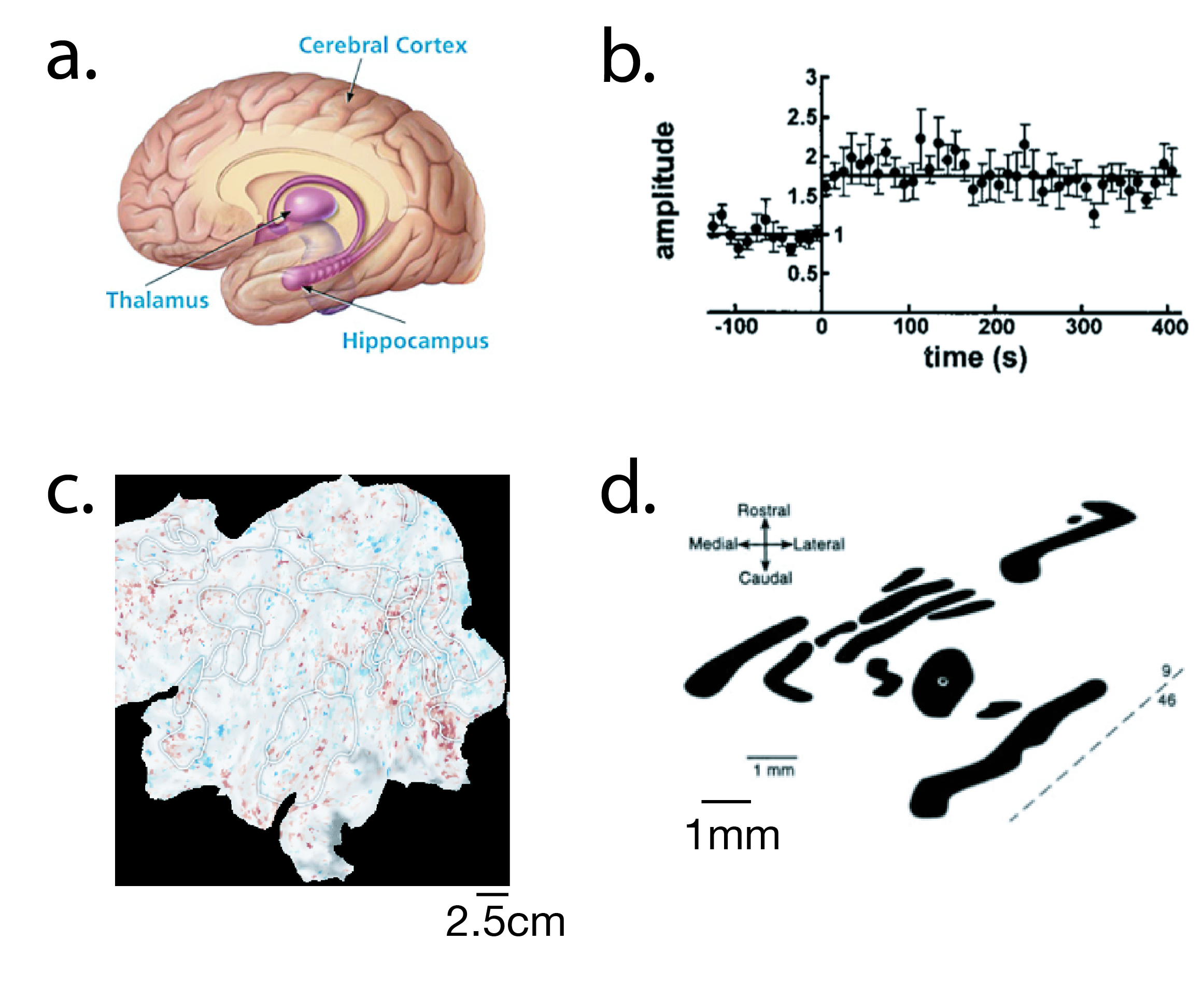
a. Cortical and hippocampal networks are potential candidates for the implementation of working memory.
b. Synaptic changes due to learning are not gradual but rather consist of switch-like events. Y-axis shows the efficiency with which a synapse conveys a signal from one neuron to another. At t=0, a stimulation protocol is applied to trigger a synaptic change.
c. Abstract items are represented in a distributed manner across cortex: flattened piece of cortex where red and blue spots represent active and suppressed areas observed with fMRI as a human subject is viewing a ‘computer’ in a movie scene.
d. Anatomical studies of cortex have revealed a modular network. Flattened piece of a monkey’s cortex where black areas are connected to each others, while surrounding white areas are not.
.
.
Attractor neural network for cognitive maps
The term cognitive map has been introduced by psychologists in the late 40’s to describe a mental representation encoding a set of items together with their relationships. Neural correlates of cognitive maps have been well characterized in the specific context of spatial navigation. For instance with the discovery of grid-cells in enthorinal cortex that encode the spatial position of an animal thanks to their peculiar receptive fields paving space with hexagonal patterns. Attractor neural networks have been proposed to account for these activities. While it was initially thought that neurons of the enthorinal cortex sustain a unique cognitive map, this view has been put into questions by recent results showing that these cells code also for other continuous spaces (such as sound frequency space or more abstract spaces) with hexagonal receptive fields as found for the coding of physical space. This raises the question of whether an attractor neural network can support multiple manifolds with grid-cell receptive fields. With Davide Spalla, Sophie Rosay, Alessandro Treves and Rémi Monasson, we have shown that indeed multiple manifolds on which single units have grid-cells receptive fields can be stored in an attractor neural network. We have moreover showed that under other functional constraints the peculiar geometry of grid-cell receptive fields is optimal for supporting the storage of multiple maps.