Analysis of artificial
neural networks
.
.
Recently developed machines reaching the best performance in a variety of tasks such as language translation or control problems are neural networks. Compared to their biological counterparts, these artificial networks have the amazing advantage, to be fully accessible, e.g. the activity of all units can be monitored while the task is being performed. Despite their accessibility, they are non-linear high-dimensional systems and it remains challenging to understand their behavior. Exploiting recent theoretical results on the dynamics of networks of rate units,
I have developed, together with Srdjan Ostojic, a method that allows to fully understand how trained networks perform their tasks. This powerful tool allows to gain insight into the emergence of cognitive functions from neural network structure and dynamics.
Disentangling the roles of dimensionality and cell classes in neural computation
A.M. Dubreuil, A. Valente, F. Mastrogiuseppe, S. Ostojic
NeurIPS Workshop, 2019
Minimal-dimensionality implementation of behavioral tasks in recurrent networks
Computational and Systems Neuroscience, 2019
Travel grant awarded to the 20 abstracts with highest reviewing scores out of >1000 submissions.
I am interested in using this tool to open the black-boxes used in AI applications. And more generally, to take advantage of the theoretical tools developed in the computational neuroscience community over the last thirty years to shed light on the mechanistic principles at stake in the functioning of modern machines.
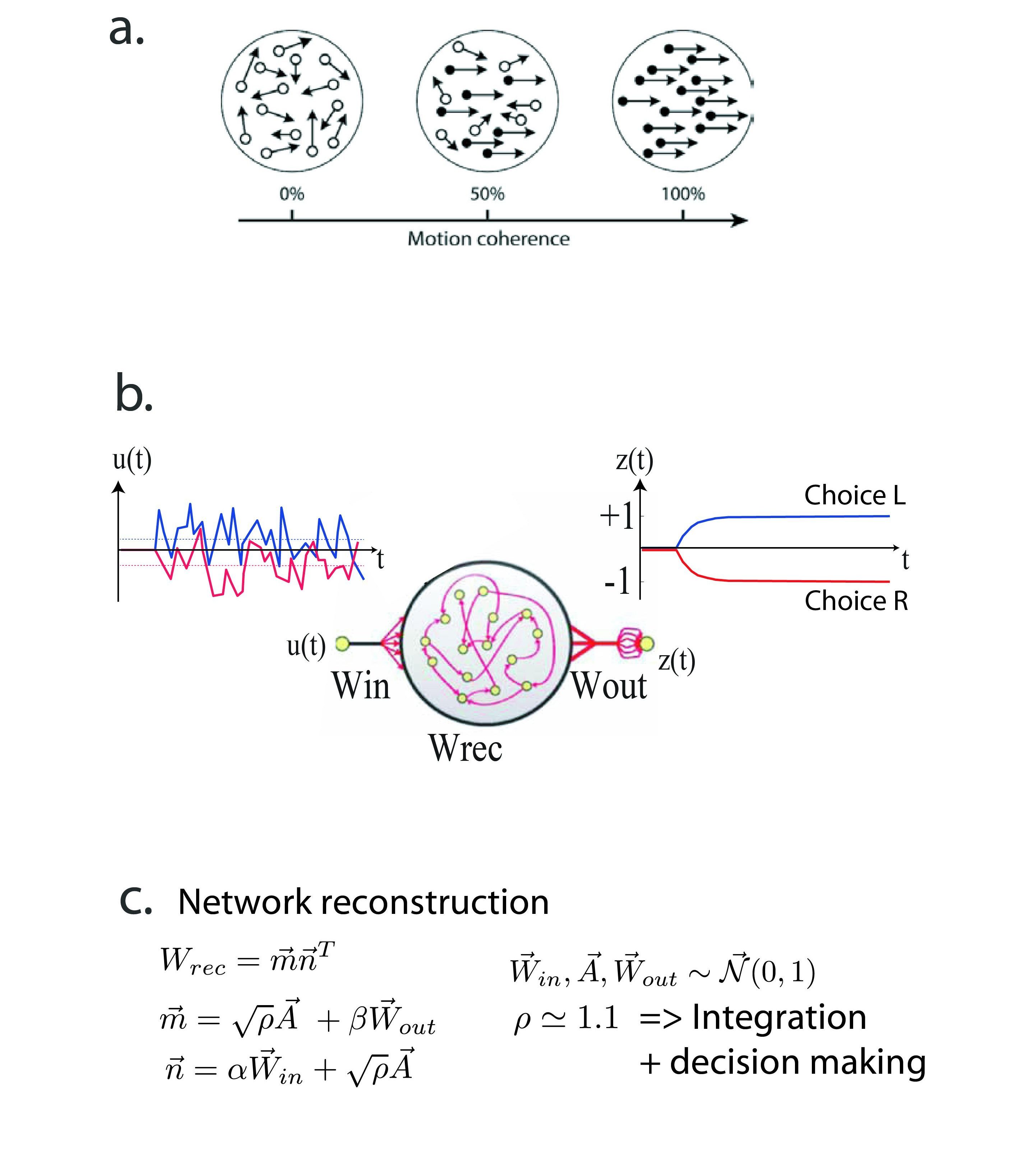
a. Schematic of a behavioral task used to study perception in neuroscience experiments. Dots moving erratically with a certain amount of motion coherence towards left or right (right here) are displayed on a screen. At each trial, whose difficulty is controlled by the amount of motion coherence, the subject has to decide whether on average dots move to the right or the left.
b. An artificial neural network can be trained to perform this task. Training is done by performing gradient descent on the weights of the network to minimize a cost function defined by desired values of the output unit z(t) (modeling decision of the network) given inputs u(t) (modeling motions of the dot).
c. Once trained, the method we propose allows to reverse-engineer trained networks. As a testimony that we fully understand how a task is performed, we re-construct, by hand, networks implementing the task. This is done by proposing a class of network connectivities, as in standard computational modeling work, that solve the task at hand.